自然循环系统模型分析
图6-3为自然循环式热水系统示意图。
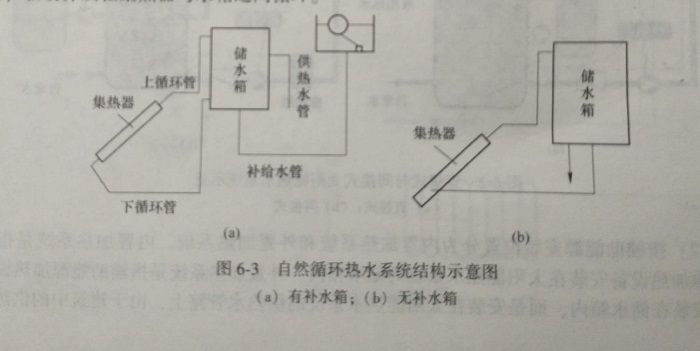
在自然循环系统中，其瞬时流量取决于各瞬间的热虹吸压头，而热虹吸压头又与系统的温度分布有关，且随时间而变化，集热器的进口水温取决于储水箱中的温度分布，而储水箱中的水温又随时间变化，因此在研究分析自然循环式太阳热水系统的工作性能时，要作出一些必要的假设。
假定集热器与储水箱中的水温分布均为线性的，它们的平均温度分别为Tm和Tn，且集热器的热容很小，可以忽略不计。因此，集热器的能量平衡方程为
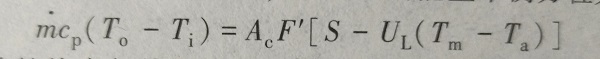(6-1)假定上、下循环管的热容与热损均很小，可以忽略，且储水箱中的平均水温与箱体的平均温度相等，则储水箱的能量平衡方程为
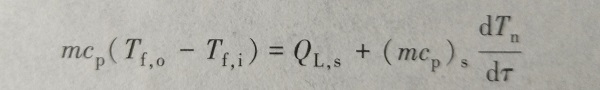(6-2)实验测定，在一天的大部分时间内，集热器的平均温度与储水箱的平均水温非常接近，故可进一步假设Tm＝Tn，因此有
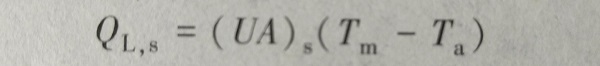(6-3)式中，Tm代表系统的平均温度;QL,S为储水箱的热损失，可表示为
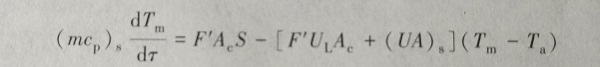(6-4)将式(6-3)代入式(6-2)，即得
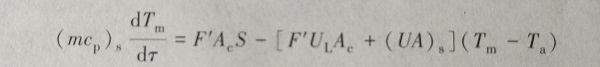(6-5)已知驱动力S和环境温度Ta随时间变化的函数关系时，式(6-5)可作为时间的函数从而解得Tm，解出Tm以后，可进一步计算系统的流量，计算的依据是:在准稳态下，每一瞬时系统的热虹吸压头hT与流动阻力损失水头hf相平衡。即
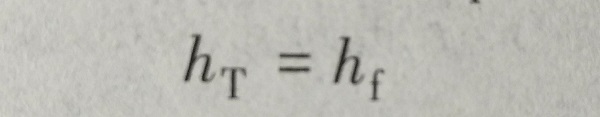(6-6）hT可由系统的温度分布来确定，如图6-4所示。hT即等于图6-4(b)中12345所围的面积。
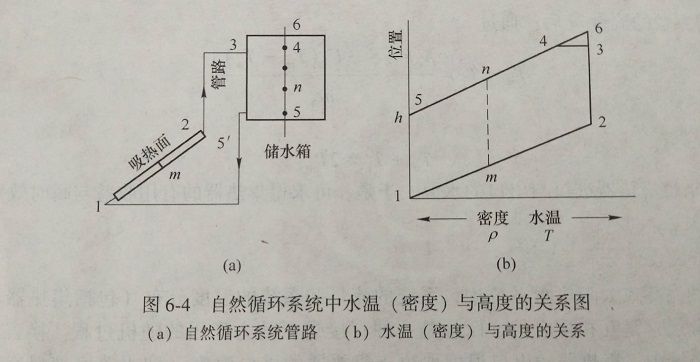
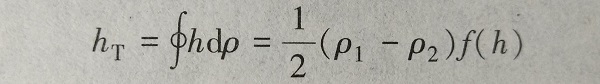(6-7)式中，ρ为系统中水的密度，f(h)为位置的函数。
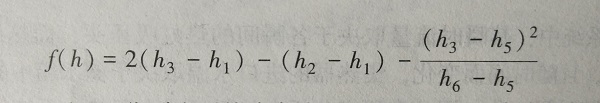(6-8)式中，h1，h2，h3，h5和h6分别为系统中各点相对于基在面的高度。假定水的密度随温度变化的关系为二次曲线，即ρ＝AT2+BT+C(A，B，C均为常数)，则式(6-7)可写为
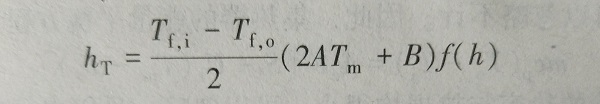(6-9)流动阻力损失水头hf为沿程阻力损失与局部阻力损失之和
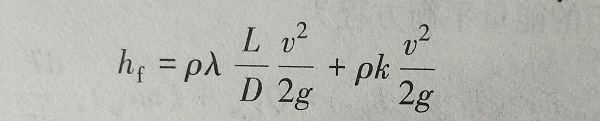(6-10)在层流状态时，管内沿程阻力系数λ为
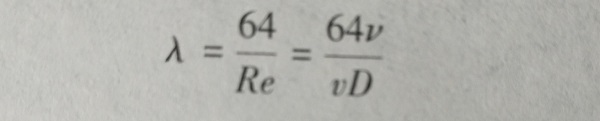(6-11)对于圆管流速v为
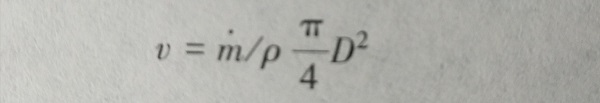(6-12)
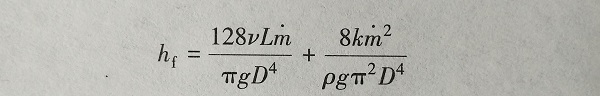(6-13)将式(6-13)和式(6-9)代入式(6-6)，并根器集热器能量平衡方程式(6-1)，整理后可得
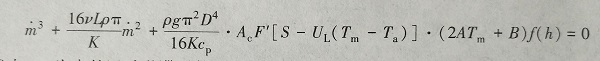(6-14)式中，v为水的运动黏滞系数；L和D分别为管道的长度和直径。
当系数确定后均为定值，解上述m的三次方程即可求得m。
求得系数的流量后，通过
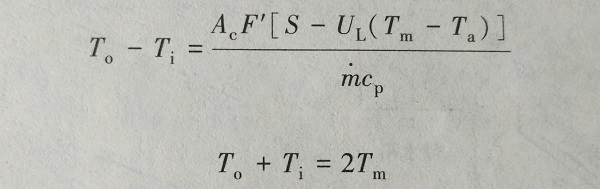
可进一步求得集热器进口与出口的水温，于是，可求得集热器的有用收益与时效率随时间的变化关系。
%%7B3RV%7DPVUT0W@SL%6VJNA.jpg)
